Ich beginne mit einem Rätsel: Stellen Sie sich vor, Sie gehen über den Campus einer großen Universität und treffen einen Mann, nennen wir ihn Tom. Sie unterhalten sich ein paar Minuten mit Tom und stellen fest, dass er schüchtern ist. Er nimmt nicht sehr oft Augenkontakt auf. Er murmelt vor sich hin. Meine Frage an Sie lautet: Wenn Sie raten müssten, würden Sie vermuten, dass Tom eher in einem mathematischen Doktoranden-Programm oder an einem Wirtschaftsstudiums teilnimmt?
Gehen wir davon aus, in diesem vereinfachtem Beispiel, dass es das eine oder das andere sein muss. Ich weiß nicht, was Sie vermutet haben, aber die meisten Leute vermuten, dass Tom eher ein Doktorand der Mathematik ist. Der Grund dafür ist, dass Schüchternheit bei promovierten Mathematikern viel häufiger vorkommt als bei Wirtschaftsstudenten. Haben Sie das auch vermutet oder haben Sie sich erstmal weitere Fragen gestellt?
Ich denke, diese Beobachtung ist zutreffend, aber es gibt noch eine andere Information, die wichtig ist und die man bei der Beantwortung dieser Frage gerne vergisst. Wie viele promovierte Mathematiker gibt es im Verhältnis zu den Studenten der Wirtschaftswissenschaften?
Es gibt viel weniger, die Zahlen variieren von Uni zu Uni, aber es sind etwa zehnmal so viele Wirtschaftsstudenten wie Mathematik-Doktoranden. Wir haben also diese beiden Informationen, dass es viel mehr Wirtschaftsstudenten als Mathematikstudenten gibt und dass Schüchternheit unter Mathematikstudenten weiter verbreitet ist als unter Wirtschaftsstudenten. Die Frage ist, wie wir diese beiden Informationen kombinieren können, um eine Gesamtschätzung über Tom zu erhalten.
Nun, hier kommt nun die Mathematik ins Spiel.
So you can imagine that this divided rectangle represents the relative proportions of math to business students, very roughly speaking. We'll put it at one to ten and now looking just at math students we can ask how common is shyness. I would very roughly guess that it's about 75% of math PhD students come off as shy. Now looking just at business school students again guessing roughly I'd say about 15% of business school students come off as shy. So now we'verepresented both of those pieces of information in one diagram and we want to know whether tom is more likely to be in a math program or a business program. We don't know which one he's in but we do know that he's shy which means that he must be in one of those green rectangles, because those represent the shy math and the shy business students. So to get a sense of the relative probabilities of him being in math versus business, we just have to compare the relative sizes of those green rectangles and it looks roughly like the green business rectangle is about twice as big as the green math rectangle.
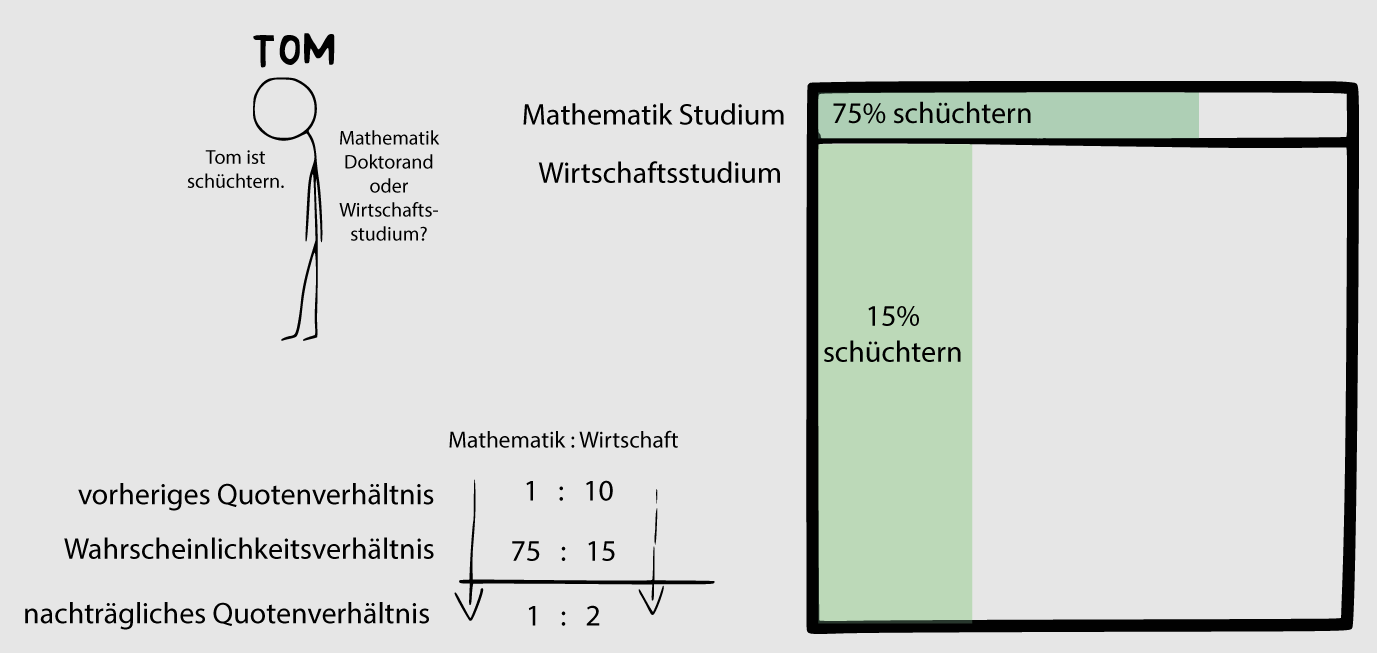
Sie sehen, wie die Rechnung aufgeht: Wir haben einfach zwei lineare Verhältnisse multipliziert - das Verhältnis von Mathematik- zu Wirtschaftsstudenten, das wir mit eins zu zehn beziffern, und das Verhältnis von Schüchternheit in Mathematik zu Schüchternheit in Wirtschaft, das wir mit 75 zu 15 beziffern, und die Multiplikation dieser beiden linearen Verhältnisse ergibt ein Flächenverhältnis, das etwa eins zu zwei beträgt. Es ist also etwa doppelt so wahrscheinlich, dass Tom im Wirtschaftsstudium ist, obwohl Schüchternheit bei Mathematikstudenten häufiger vorkommt.
So funktioniert die Mechanik der Bayes-Regeln! Und wir haben in einem einfachen Beispiel gezeigt, wie Mathematik unsere Entscheidungen und Einschätzungen beeinflussen kann. Übrigens der Satz von Bayes sieht so aus:
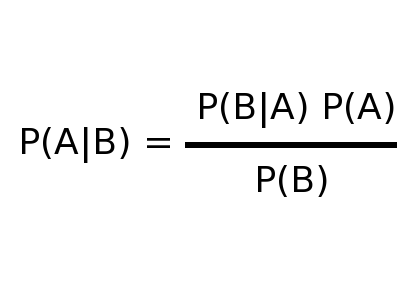
Jetzt möchte ich darüber sprechen, wie ich sie in meinem täglichen Denken verwende. Ich setze keine Zahlen in eine Formel ein. Ich zeichne diese Diagramme eigentlich fast nie, aber es gibt ein paar Regeln und Denkprinzipien, die sich aus der Mathematik der Bayes-Regel ergeben und wirklich nützlich sind.
Der erste Grundsatz lautet: Vergessen Sie nicht Ihre Vorannahmen. Wie Sie am Beispiel von Tom gesehen haben, konzentrieren sich die Leute natürlich auf den Beweis, dass Tom schüchtern ist, und vergessen die Vorannahmen. Das Hintergrund Wissen, dass Mathematik ein viel selteneres Studienfach ist als Wirtschaft. Das ist ein sehr häufiges Phänomen. Das nennt man "Prävalenzfehler".
Eine ältere Frau erzählte Folgendes: Sie musste einen Handwerker anrufen, um den Herd zu reparieren und er machte sie ein wenig nervös, denn während er da war, bemerkte sie, dass er in verschiedene Räume des Hauses spähte und es gibt keinen Grund, warum man das Schlafzimmer eines Hauses sehen sollte, wenn man hier ist, um den Herd zu reparieren. Sie hatte Geschichten gehört, in denen Handwerker nach der Reparatur zurückkamen und ein Haus ausraubten, nachdem sie die Gelegenheit hatten, den Herd zu reparieren und so war sie besorgt, dass dies in diesem Fall der Fall war. Ich denke, wenn man sieht, dass der Handwerker herumschnüffelt, könnte die Möglichkeit bestehen das er einen ausrauben wird. Sie hätte aber einen Schritt zurücktreten und sich daran erinnern sollen, wie groß die Wahrscheinlichkeit ist, dass ein Handwerker ehrlich ist, im Gegensatz zu einem Einbrecher. Ich denke, dass es nicht so häufig vorkommt, dass jemand ein Einbrecher ist. Ich kenne die genauen Zahlen nicht, aber vielleicht gibt es hundertmal mehr ehrliche Handwerker als Räuber, etwa in dieser Größenordnung. Selbst wenn man also davon ausgeht, dass die Schnüffelei unter Räubern viel verbreiteter ist als unter ehrlichen Reparaturarbeitern, würden wir sagen, dass 80 % der Räuber beim Schnüffeln gesehen werden und vielleicht 10 % der ehrlichen Reparaturarbeiter. Die Wahrscheinlichkeit, dass dieser Mann sie ausrauben will, steigt dadurch nur von vielleicht 1 % auf vielleicht 8 %. Sie sollte also ihre Türen abschließen, aber nicht ausflippen.
Grundsatz Nummer zwei möchte ich mit einer anderen Geschichte illustrieren. Vor einiger Zeit arbeitete ich mit einem Mann namens, nennen wir ihn Bob und ich hatte Grund zu der Annahme, dass Bob auf eine andere Person, die mit uns zusammenarbeitete, nennen wir sie Alice, eifersüchtig ist oder mit ihr konkurrieren könnte. Eines Tages trank ich mit Bob einen Kaffee und er beschwerte sich über Alice, weil sie einige Projekte nicht fertiggestellt hatte, die sie zu diesem Zeitpunkt hätte fertigstellen sollen. Ich denke mir, das beweist nur, dass ich mit Bob richtig lag. Wenn er eifersüchtig wäre, würde er sie schlecht aussehen lassen wollen und er beschwert sich über sie. Ich habe also recht. Kurze Zeit später kam mir die Frage in den Sinn: Nun gut, nehmen wir einmal an, dass ich falsch liege und Bob nicht eifersüchtig auf Alice ist. Wie unwahrscheinlich ist es in diesem Szenario, dass er sich über sie beschwert und das nicht ungeplant. Eigentlich sehr plausibel. Es kommt oft vor, dass Menschen sich darüber ärgern, wenn jemand etwas nicht zu Ende bringt, was er eigentlich zu Ende bringen sollte und das hat nichts mit Eifersucht zu tun. Ich mag also immer noch meine Gründe haben, um zu vermuten, dass Bob eifersüchtig auf Alice ist oder mit ihr konkurriert, aber wenn ich diesen neuen Beweis sehe, sollte ich mich nicht wesentlich sicherer fühlen, dass ich Recht habe. Vielleicht ist es in der Welt, in der er auf Alice eifersüchtig ist, etwas wahrscheinlicher, dass er sich über sie beschwert, als in der Welt, in der er es nicht ist. Aber nur ein bisschen. Die Wahrscheinlichkeit, dass ich Recht hatte, dürfte sich dadurch nicht wesentlich ändern. Ich glaube, das ist auch eine sehr häufige Sache, dass wir durch die Welt gehen und Beweise sehen, die wir mit unserer aktuellen Theorie und unserer Lieblingstheorie erklären können und das macht uns umso sicherer, dass wir Recht haben. Wir machen nicht den zusätzlichen Schritt, uns zu fragen, was wäre, wenn ich falsch läge?
Nehmen wir an, ich gebe jemandem ein Papier oder eine Idee zur Bewertung und er findet sie großartig. Ich muss mich dann fragen, wie häufig es vorkommt, dass er schlechte Ideen für großartig hält. Wie sehr ist seine Zustimmung ein Beweis dafür, dass meine Idee tatsächlich großartig ist? Das ist also Grundsatz Nummer zwei: Fragen Sie sich, was wäre, wenn ich mich irren würde, was würde ich erwarten und wie unterscheidet es sich von dem, was ich derzeit sehe.
Grundsatz Nummer drei ist sozusagen die Kehrseite von Grundsatz Nummer zwei, den man auch als inkrementelle Aktualisierung bezeichnen könnte.
Wenn ich im Laufe der Zeit auf weitere kleine bis mittelgroße Beweise stoße, die alle in der Welt, in der etwas funktioniert, wahrscheinlicher sind als in der Welt, in der es nicht funktioniert. Sollte ich meine Meinung allmählich ändern. Vielleicht wird es einen Wendepunkt geben, an dem es insgesamt wahrscheinlicher ist, dass etwas funktioniert als, dass es nicht funktioniert. In Anbetracht all der Beweise, auf die ich gestoßen bin, und ich denke, es ist wichtig, auf diese Schneeflocken von Beweisen zu achten, die für sich genommen vielleicht nur sehr wenig wiegen, aber wenn man sie beachtet und bemerkt, wie sie sich allmählich anhäufen, wird ihr kollektives Gewicht groß genug, um einen Ast zu brechen. Das ist also Grundsatz Nummer drei: Schritt für Schritt aktualisieren.
